Segundo encuentro

Contenidos:

Desvío o error

Desvío Medio

Error cuadrático total

Varianza

Desvío Típico o estándar

Indice de coeficiente de variación 

Seguimos trabajando con la distribución del primer encuentro

Desvío o error

Como calcular el error o desvío de casa variable

Para Erika el desvío de su puntaje es:   78 - 78,17 = -0,17

Si sumamos todos los desvíos el resultado es 0. (comprobar)

La formula para el Desvío es:   e= Variable - Media Aritmética 

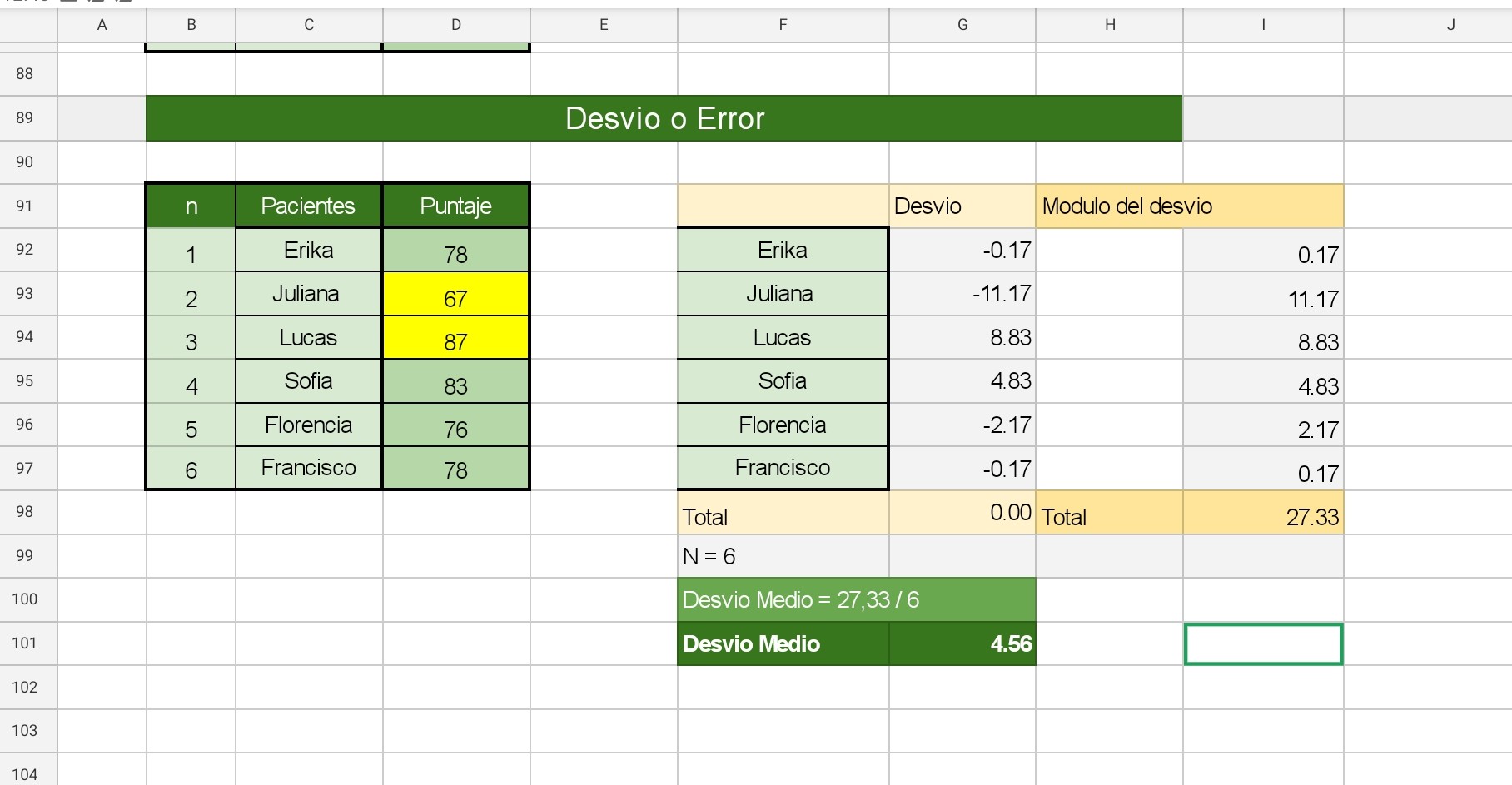
Desvío Medio

Determina que promedio se esta desviando la variable en la distribución.

"Piensen que pasaría si todos tuvieran el mimo puntaje..."

Es el promedio del modulo de cada error o desvío.

Modulo del error: |error|

Entonces convertimos todos los errores con signo positivo, generado por la función modulo.

Luego se calcula ese promedio, y ese es el Desvío Medio

Veamos el ejemplo: 

Varianza

La varianza permite comparar entre dos o mas muestras el nivel de dispersión de los datos, a mayor varianza mayor es la dispersión en los datos, o existen valores muy alejados de la media aritmética, es decir del promedio.

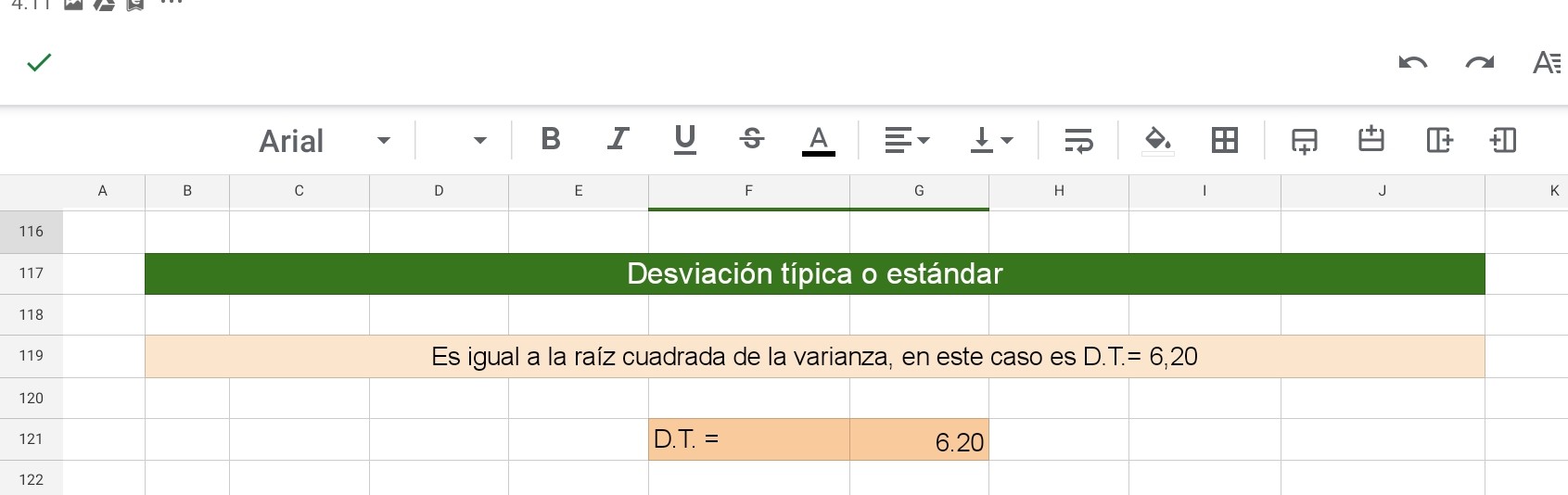
Desvío Típico

El desvío típico permite comparar la concentración de los datos respecto a la media aritmética; a menor desviación típica mayor es la concentración de los datos en la muestra.

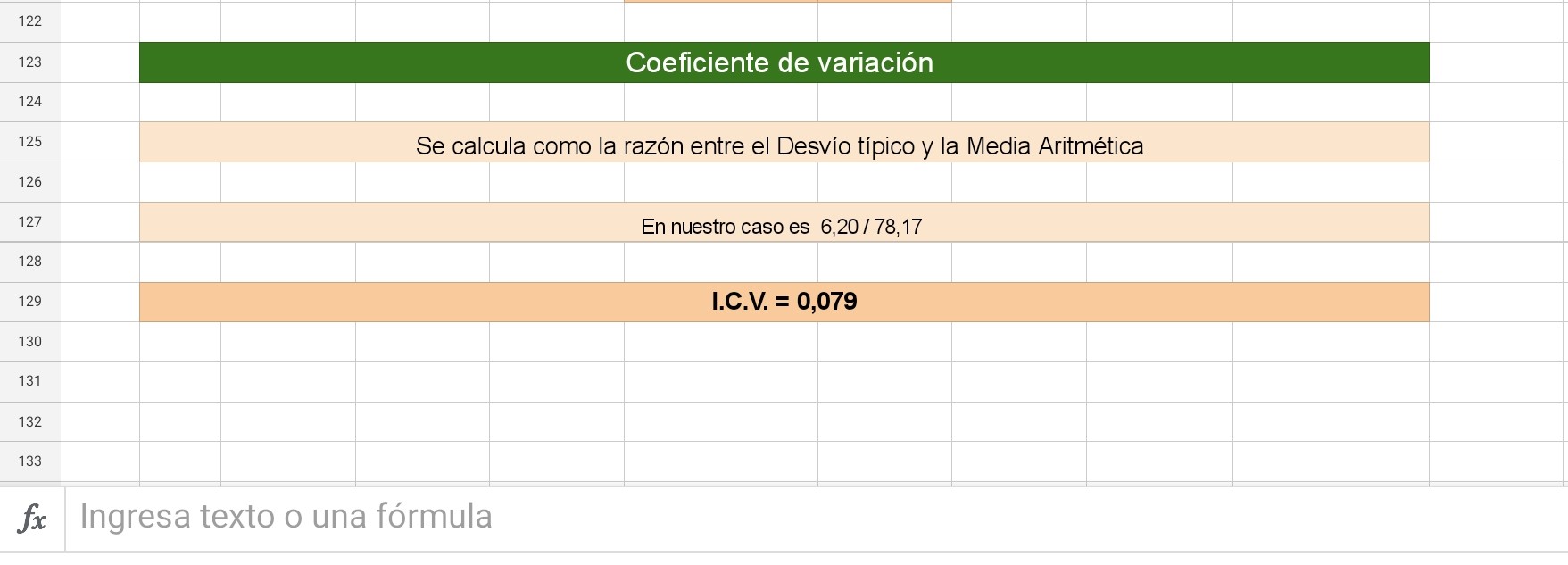
Coeficiente de variación

El coeficiente de variación permite establecer entre varias muestras, cuál se mantiene mas homogénea, este valor se lo compara con el Indice de Coeficiente de variación de la distribución Normal que es de 0,33, cuanto mas cerca esté de este valor más homogénea será la distribución.

El concepto de Distribución Normal lo veremos en el transcurso de la cursada, por el momento simplemente esperamos que puedan calcular los parámetros.