Sexto encuentro

Desvío para datos agrupados

Seguimos con el estudio de la distribución del quinto encuentro, donde ya encontramos algunos parámetros, para calcular los devíos usaremos la Media aritmética para marca de clase, el desvío o error y la frecuencia absoluta.

Desvío Medio

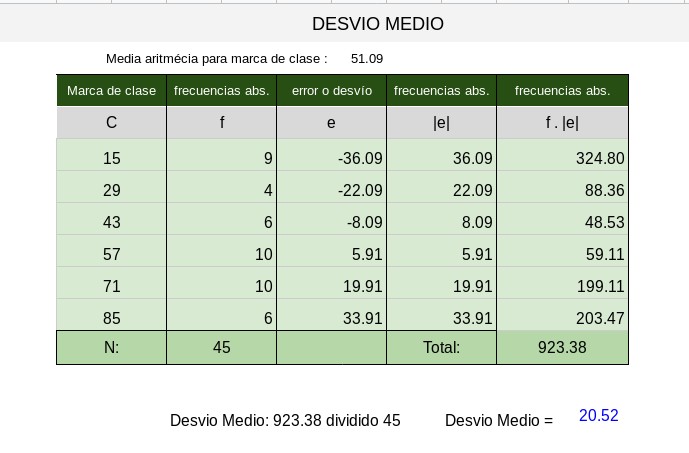
Recordemos que el error es la variable menos la media aritmética, en este caso se tomo la marca de clase como variable y restamos la media aritmética para marca de clase calculada.

Cuando analizamos datos agrupados debemos tener en cuenta que el error esta multiplicado por la frecuencia que ocurre en ese intervalo.

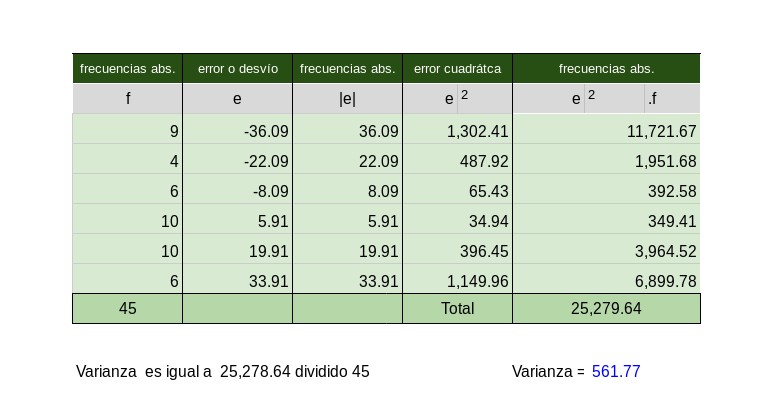
Calculo de Varianza

Al igual que en la distribución en una serie, se debe elevar al cuadrado el error o desvío, y luego multiplicar por la frecuencia, que son las veces que se repite ese error en el intervalo.

La varianza es el promedio de los errores cuadráticos, que indica al comparar con otra muestra tomada si existen valores muy alejados de la media aritmética.

A mayor varianza mayor es la dispersión de los datos.

Desvío Típico:

El desvio Típico se calcula realizando la raíz cuadrada de la varianza, en este caso el parámetro indica que a menos desviación típica mayor concentración de datos respecto a la media aritmética.

D.T = Raiz cuadrada de 561.77

D.T = 23.70

Indice de Coeficiente de variación

En este caso simplemente es el cociente entre el desvío típico y la media aritmética.

I.C.V = Desvio Típico / Media aritmética para marca de clase

I.C.V = 23.70 / 51.09

I.C.V = 0.46

El Coeficiente expresado en porcentaje es I.C.V * 100

en nuestro caso: C.V.% = 46 %

Lo que nos esta indicando que el desvio típico es un 46% del promedio.

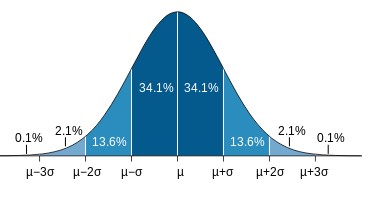
Las distribuciones donde el C.v. se aproxima al 33% de la media aritmética son las distribuciones mas homogéneas.

Las distribuciones mas homogeneas son las que presentan en la distribución de frecuencias una curva que tiende a ser acampanada, como se muestra en la siguiente figura.